Soal dan pembahasan OSN Kabupaten

 Kemampuan Dasar

Pada bagian ini setiap jawaban yang benar bernilai $2$ poin dan setiap jawaban yang salah atau kosong bernilai nol.

Soal Nomor 1
Misalkan $f\left(x\right)=\frac{3(x-1)(x-2)}{2}+\frac{(x-2)(x-3)}{2}$ $-2(x-1)(x-3)$. Nilai dari $f\left(20\right)$ adalah $\cdots \cdot$

Pembahasan

Cara 1: Menyederhanakan dulu
Kita sederhanakan rumus fungsi $f\left(x\right)$, lalu substitusi $x=20$.
$$\begin{array}{cc}f\left(x\right)& =\frac{3(x-1)(x-2)}{2}+\frac{(x-2)(x-3)}{2}-2(x-1)(x-3)\\ & =\frac{3(x^2-3x+2)}{2}+\frac{x^2-5x+6}{2}-2(x^2-4x+3)\\ & =\frac{3x^2-9x+6+x^2-5x+6}{2}-2x^2+8x-6\\ & =\frac{4x^2-14x+12}{2}-2x^2+8x-6\\ & =2x^2-7x+6-2x^2+8x-6=x\end{array}$$Karena $f\left(x\right)=x$, maka untuk $x=20$, diperoleh $f\left(20\right)=20$
Cara 2: Substitusi langsung
Substitusi langsung $x=20$ pada $f\left(x\right)$.
$$\begin{array}{cc}f\left(20\right)& =\frac{3(20-1)(20-2)}{2}+\frac{(20-2)(20-3)}{2}-2(20-1)(20-3)\\ & =\frac{3\left(19\right)\left({18}^9\right)}{2}+\frac{\left({18}^9\right)\left(17\right)}{2}-2\left(19\right)\left(17\right)\\ & =3\left(19\right)\left(9\right)+9\left(17\right)-2\left(19\right)\left(17\right)=20\end{array}$$Jadi, nilai dari $f\left(20\right)=20$
Catatan:
Substitusi langsung $x=20$ pada $f\left(x\right)$ masih sangat memungkinkan untuk dilakukan perhitungan, tetapi akan memakan waktu yang lama bila $x$ disubstitusi sebagai bilangan yang lebih besar, misalnya $x=2020$. Cara yang disarankan adalah menyederhanakan rumus fungsi $f\left(x\right)$ sebisa mungkin.

Soal Nomor 2
Diberikan sebuah kubus besar berukuran $3\times 3$ yang seluruh permukaannya dicat dengan warna merah. Kubus tersebut dipotong menjadi $27$ kubus satuan (kubus berukuran $1\times 1\times 1$). Diketahui bahwa Amir mengambil satu kubus kecil yang salah satu sisinya berwarna merah. Peluang kubus kecil yang diambil Amir memiliki tepat dua sisi berwarna merah adalah $\cdots \cdot$

Pembahasan

Banyak kubus yang tidak terkena cat untuk kubus berukuran $n\times n\times n$ adalah $(n-2)(n-2)(n-2)$, sedangkan banyak kubus yang terkena cat satu sisi saja adalah $6(n-2)(n-2)$, serta banyak kubus yang terkena cat tepat $3$ sisi adalah $8$ (di tepi kubus).
Untuk $n=3$, banyak kubus yang tidak terkena cat ada $1$ buah sehingga sebanyak $26$ kubus yang terkena cat.
Selanjutnya, terdapat $6(3-2)(3-2)=6$ kubus yang terkena cat satu sisi saja. Akibatnya, banyak kubus yang terkena cat dua sisi adalah $26-6-8=12$, seperti tampak pada ilustrasi gambar berikut.

Dengan demikian, peluang terambilnya kubus kecil dengan tepat dua sisi terkena cat adalah $\frac{12}{26}=\frac{6}{13}$

Soal Nomor 2
Diberikan sebuah kubus besar berukuran $3\times 3$ yang seluruh permukaannya dicat dengan warna merah. Kubus tersebut dipotong menjadi $27$ kubus satuan (kubus berukuran $1\times 1\times 1$). Diketahui bahwa Amir mengambil satu kubus kecil yang salah satu sisinya berwarna merah. Peluang kubus kecil yang diambil Amir memiliki tepat dua sisi berwarna merah adalah $\cdots \cdot$

Pembahasan

Soal Nomor 3
Diberikan trapesium siku-siku seperti pada gambar di bawah ini.

Jika $AB=1,BD=\sqrt{7}$, dan $AD=CD$, maka luas trapesium tersebut adalah $\cdots \cdot$

Pembahasan

Tarik garis dari titik $A$ sehingga tegak lurus dengan $DC$, memotong di titik $E$ seperti gambar.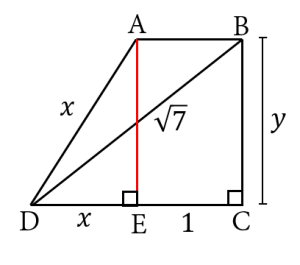

Diketahui $AB=EC=1$. Misalkan $AD=x$, maka $DE=x-1$. Misalkan juga $AE=BC=y$.
Pada segitiga siku-siku $ADE$, berlaku rumus Pythagoras.
$\begin{array}{cccc}A{E}^2& =A{D}^2-D{E}^2& & \\ y^2& =x^2-(x-1{)}^2& & \\ y^2& =x^2-(x^2-2x+1)& & \\ y^2& =2x-1& & (\cdots 1)\end{array}$
Pada segitiga siku-siku $BDC$, juga berlaku rumus Pythagoras.
$\begin{array}{cccc}B{C}^2& =B{D}^2-D{C}^2& & \\ y^2& =(\sqrt{7}{)}^2-x^2& & \\ y^2& =7-x^2& & (\cdots 2)\end{array}$
Berdasarkan $\left(1\right)$ dan $\left(2\right)$, diperoleh
$\begin{array}{cc}2x-1& =7-x^2\\ x^2+2x-8& =0\\ (x+4)(x-2)& =0\end{array}$
Didapat $x=-4$ (tidak memenuhi karena bernilai negatif) atau $x=2$.
Substitusi $x=2$ pada persamaan $\left(1\right)$ sehingga diperoleh
$y^2=2\left(2\right)-1\Rightarrow y=\sqrt{3}$
Luas trapesiun $ABCD$ selanjutnya dinyatakan oleh
$\begin{array}{cc}{L}_{ABCD}& =\frac{(AB+CD)\times BC}{2}\\ & =\frac{(1+2)\times \sqrt{3}}{2}=\frac{3}{2}\sqrt{3}\end{array}$
Jadi, luas trapesium itu adalah $\frac{3}{2}\sqrt{3}$

[collapse]

Soal Nomor 4
Misalkan $x,y$ bilangan asli sehingga $2x+3y=2020$. Nilai terbesar yang mungkin dari $3x+2y$ adalah $\cdots \cdot$

Pembahasan

Perhatikan ekspresi $3x+2y$. Supaya bernilai sebesar mungkin, maka nilai $x$ harus dibuat maksimum karena koefisiennya lebih besar dari variabel $y$.
Tinjau persamaan $2x+3y=2020$.
Jika dipilih $x=1010$, berakibat $y=0$, padahal $y$ harus bilangan asli.
Nilai $x=1009$ dan $x=1008$ mengakibatkan nilai $y$ juga bukan bilangan asli.
Jika dipilih $x=1007$, diperoleh $y=2$. Artinya, nilai $x$ terbesar adalah $1007$.
Dengan demikian,
$\begin{array}{cc}3x+2y& =3\left(1007\right)+2\left(2\right)\\ & =3021+4=3025\end{array}$
Jadi, nilai terbesar yang mungkin dari $3x+2y=3025$

[collapse]

Soal Nomor 5
Suatu barisan bilangan real $a_1,a_2,a_3,\cdots$ memenuhi $a_1=1$, $a_2=\frac{3}{5}$, dan $\frac{1}{a_n}=\frac{2}{a_{n-1}}-\frac{1}{a_{n-2}}$ untuk setiap $n\ge 3$. Bilangan $a_{2020}$ dapat ditulis sebagai $\frac{p}{q}$ dengan $p$ dan $q$ bilangan asli relatif prima. Nilai $p+q$ adalah $\cdots \cdot$

Pembahasan

Diketahui $a_1=1$ dan $a_2=\frac{3}{5}$.
Untuk $n\ge 3$, berlaku $\frac{1}{a_n}=\frac{2}{a_{n-1}}-\frac{1}{a_{n-2}}$.
Cara pertama: Relasi rekurensi
Misalkan $\frac{1}{a_n}=b_n$, sehingga persamaan di atas ditulis $b_n=2b_{n-1}-b_{n-2}$. Persamaan karakteristik dari relasi rekurensi tersebut adalah
$\begin{array}{cc}{r}^2& =2r-1\\ r^2-2r+1& =0\\ (r-1{)}^2& =0\end{array}$
Jadi, diperoleh $r=1$ (kembar).
Karena memiliki akar kembar, maka solusi umum relasi rekurensi tersebut adalah $b_n=C_1{r}^2+C_{2}n{r}^2$.
Perhatikan bahwa $a_1=1$, sehingga $b_1=1$. Substitusi $n=1$ dan kita peroleh
$\begin{array}{cccc}{b}_1& =C_1(1{)}^2+C_2(1\left)\right(1{)}^2& & \\ 1& =C_1+C_2& & (\cdots 1)\end{array}$
Perhatikan juga bahwa $a_2=\frac{3}{5}$, sehingga $b_2=\frac{5}{3}$. Substitusi $n=2$ dan kita peroleh
$\begin{array}{cccc}{b}_2& =C_1(1{)}^2+C_2(2\left)\right(1{)}^2& & \\ \frac{5}{3}& =C_1+2C_2& & (\cdots 2)\end{array}$
Dari kedua persamaan yang didapat, kita mendapat $C_1=\frac{1}{3}$ dan $C_2=\frac{2}{3}$, sehingga $b_n=\frac{1}{3}+\frac{2}{3}n=\frac{1+2n}{3}$, artinya $a_n=\frac{3}{1+2n}$.
Substitusi $n=2020$ dan akhirnya didapat $a_{2020}=\frac{3}{1+2\left(2020\right)}=\frac{1}{1347}$.
Oleh karena itu, nilai $p=1$ dan $q=1347$, berarti $p+q=1348$ 
Cara kedua: Pola
Substitusi $n=3$, diperoleh
$\begin{array}{cc}\frac{1}{a_3}& =\frac{2}{a_2}-\frac{1}{a_1}\\ \frac{1}{a_3}& =\frac{2}{\frac{3}{5}}-\frac{1}{1}\\ \frac{1}{a_3}& =\frac{10}{3}-1\\ a_3& =\frac{3}{7}\end{array}$
Substitusi $n=4$, diperoleh
$\begin{array}{cc}\frac{1}{a_4}& =\frac{2}{a_3}-\frac{1}{a_2}\\ \frac{1}{a_4}& =\frac{2}{\frac{3}{7}}-\frac{1}{\frac{3}{5}}\\ \frac{1}{a_4}& =\frac{14}{3}-\frac{5}{3}\\ a_4& =\frac{3}{9}\end{array}$
Substitusi $n=5$, diperoleh
$\begin{array}{cc}\frac{1}{a_5}& =\frac{2}{a_4}-\frac{1}{a_3}\\ \frac{1}{a_5}& =\frac{2}{\frac{3}{9}}-\frac{1}{\frac{3}{7}}\\ \frac{1}{a_5}& =6-\frac{7}{3}\\ a_5& =\frac{3}{11}\end{array}$
Dari $3$ nilai yang telah didapat, tampak suatu pola barisan: $\frac{3}{7},\frac{3}{9},\frac{3}{11}$, yaitu pembilang tetap $3$, namun penyebut bertambah $2$ membentuk barisan aritmetika.
Rumus suku ke-$n$ dari barisan semula adalah $a_n=\frac{3}{2n+1}$ dengan $n\ge 3$. Pernyataan ini dapat dibuktikan menggunakan induksi matematika.
Dengan demikian,
$a_{2020}=\frac{3}{2\left(2020\right)+1}=\frac{1}{1347}$
Oleh karena itu, nilai $p=1$ dan $q=1347$, berarti $p+q=1348$

Soal Nomor 6
Diketahui $S$ adalah himpunan semua titik $(x,y)$ pada bidang Kartesius, dengan $x,y$ bilangan bulat, $0\le x\le 20$ dan $0\le y\le 19$. Banyaknya cara memilih dua titik berbeda di $S$ sehingga titik tengahnya juga ada di $S$ adalah $\cdots \cdot$
Catatan: Dua titik $P(a,b)$ dan $Q(c,d)$ berbeda jika $a\ne c$ dan $b\ne d$. Pasangan titik $(P,Q)$ dan $(Q,P)$ dianggap sama.

Pembahasan

Misalkan diberikan $P(a,b)$ dan $Q(c,d)$. Titik tengah dari $PQ$ dinyatakan oleh $M(\frac{a+c}{2},\frac{b+d}{2})$ dengan $0\le a,c\le 20$ dan $0\le b,d\le 19$. Dari sini diketahui bahwa $a$ dan $c$ harus memiliki paritas yang sama (sama-sama ganjil atau sama-sama genap), begitu juga dengan $b$ dan $d$. Banyak kemungkinan nilai untuk $a,c$ masing-masing adalah $21$, sedangkan untuk $b,d$ sebanyak $20$.

1. Jika $a,c$ keduanya ganjil, maka ada $10$ kemungkinan untuk $a$ dan $c$, sehingga banyak pasangan berbeda $(a,c)$ adalah $10\cdot 10=100$. Jika $a,c$ keduanya genap, maka ada $11$ kemungkinan $a$ dan $c$, sehingga banyak pasangan berbeda $(a,c)$ adalah $11\cdot 11=121$. Total pasangan sebanyak $100+121=221$.
2. Jika $b,d$ keduanya ganjil, maka ada $10$ kemungkinan untuk $b$ dan $d$, sehingga banyak pasangan berbeda $(b,d)$ adalah $10\cdot 10=100$. Jika $b,d$ keduanya genap, maka juga ada $10$ kemungkinan $b$ dan $d$, sehingga banyak pasangan berbeda $(b,d)$ adalah $10\cdot 10=100$. Total pasangan sebanyak $100+100=200$.

Banyak titik $M(\frac{a+c}{2},\frac{b+d}{2})$ adalah $221\cdot 200=44.200$. Karena titik $(P,Q)$ dan $(Q,P)$ dianggap sama, maka banyak pasangan $(P,Q)$ ada $\frac{44.200}{2!}=22.100$, tetapi terdapat titik $P(a,b)$ dan $Q(c,d)$ sehingga $P=Q$ (ketika $a=c$ dan $b=d$). Banyak pasangan $(P,Q)$ ketika $P=Q$ adalah $21\cdot 20=420$. Dengan demikian, diperoleh banyak cara memilih dua titik sehingga titik tengahnya juga di $S$ adalah $22.100-420=21.680$

[collapse]

Soal Nomor 7
Diketahui segitiga $ABC$ dengan panjang sisi $BC=3$, $CA=4$, dan $AB=5$. Titik $P$ terletak pada $AB$ dan $Q$ terletak di $AC$ sehingga $AP=AQ$ dan garis $PQ$ membagi segitiga $ABC$ menjadi dua daerah dengan luas yang sama. Panjang segmen $PQ$ adalah $\cdots \cdot$

Soal Nomor 8
Himpunan penyelesaian dari persamaan $|x+1|+\left|\frac{19}{x-1}\right|=\frac{20-x^2}{1-x}$ adalah interval $[a,b)$. Nilai dari $b-a$ adalah $\cdots \cdot$

Pembahasan

Diketahui $|x+1|+\left|\frac{19}{x-1}\right|=\frac{20-x^2}{1-x}$.
Berdasarkan definisi nilai mutlak, diperoleh
$\begin{array}{cc}|x+1|& =\{\begin{array}{cc}x+1,& \text{jika}x\ge -1\\ -x-1,& \text{jika}x<-1\end{array}\\ |x-1|& =\{\begin{array}{cc}x-1,& \text{jika}x\ge 1\\ -x+1,& \text{jika}x<1\end{array}\end{array}$
Kasus 1: $x<-1$
Setelah dibatasi nilai $x$ dalam interval $x<-1$, kita peroleh
$\begin{array}{cc}(-x-1)+\frac{19}{-x+1}& =\frac{20-x^2}{1-x}\\ \text{Kalikan kedua ruas}& \text{dengan}(1-x)\\ (-x-1)(1-x)+19& =20-x^2\\ x^2-1+19& =20-x^2\\ 2x^2& =2\\ x& =\pm 1\end{array}$
Karena $x=\pm 1$ tidak masuk interval $x<-1$, maka untuk kasus ini, tidak ada nilai $x$ yang memenuhi.
Kasus 2: $-1\le <x<1$
Setelah dibatasi nilai $x$ dalam interval $-1\le x<1$, kita peroleh
$\begin{array}{cc}(x+1)+\frac{19}{-x+1}& =\frac{20-x^2}{1-x}\\ \text{Kalikan kedua ruas}& \text{dengan}(1-x)\\ (x+1)(1-x)+19& =20-x^2\\ -x^2+1+19& =20-x^2\\ 20& =20\end{array}$
Pernyataan terakhir bernilai benar, artinya persamaan tersebut terpenuhi untuk semua $x\in R$. Nilai $x$ yang memenuhi untuk kasus ini adalah $-1\le x<1$ (syarat intervalnya).
Kasus 3: $x\ge 1$
Setelah dibatasi nilai $x$ dalam interval $x\ge 1$, kita peroleh
$\begin{array}{cc}(x+1)+\frac{19}{x-1}& =\frac{20-x^2}{1-x}\\ \text{Kalikan kedua ruas}& \text{dengan}(x-1)\\ (x+1)(x-1)+19& =-20+x^2\\ x^2-1+19& =-20+x^2\\ 18& =-20\end{array}$
Pernyataan terakhir bernilai salah, artinya persamaan tersebut tidak terpenuhi untuk semua $x\in R$. Kita simpulkan bahwa tidak ada nilai $x$ yang memenuhi untuk kasus ini.
Dari ketiga kasus, kita peroleh bahwa himpunan penyelesaiannya adalah nilai-nilai $x$ dalam interval $-1\le x<1$ atau dalam notasi selang ditulis $[-1,1)$, berarti $a=-1$ dan $b=1$, sehingga $b-a=1-(-1)=2$

[collapse]

Soal Nomor 9
Misalkan $n\ge 2$ bilangan asli sedemikian sehingga untuk setiap bilangan asli $a,b$ dengan $a+b=n$ berlaku $a^2+b^2$ merupakan bilangan prima. Hasil penjumlahan semua bilangan asli $n$ semacam itu adalah $\cdots \cdot$

Soal Nomor 10
Suatu komite yang terdiri dari beberapa anggota hendak menghadiri $40$ rapat. Diketahui bahwa setiap rapat dihadiri tepat $10$ anggota komite dan setiap dua anggota menghadiri rapat bersama paling banyak satu kali. Banyaknya anggota komite terkecil yang mungkin adalah $\cdots \cdot$